The experimental investigation of probability is a current infrastructure. Betting demonstrates that there has been an investment in quantifying the thoughts of chance for centuries, anyway correct scientific depictions emerged much later. There are explanations obviously, for the moderate improvement of the arithmetic of chance. While diversions of chance furnished the impulse for the numerical investigation of likelihood, crucial issues are still darkened by the superstitions of gamblers.
Related posts:
RS Trigonometry - Definition
Trigonometry nuts and bolts are regularly showed in school either as a unattached course or as a component of a precalculus course. The trigonometric roles are pervasive in parts of immaculate math and connected science for example Fourier investigation and the wave comparison, which are in turn crucial to a considerable number of extensions of science and mechanics. Circular trigonometry studies ...
Trigonometry nuts and bolts are regularly showed in school either as a unattached course or as a component of a precalculus course. The trigonometric roles are pervasive in parts of immaculate math and connected science for example Fourier investigation and the wave comparison, which are in turn crucial to a considerable number of extensions of science and mechanics. Circular trigonometry studies ...
QS Statistics (1)
Statistics is the investigation of the gathering, group, examination, understanding, and presentation of data. It manages all viewpoints of this, incorporating the arranging of information accumulation in terms of the outline of overviews and investigations.
Statistics is the investigation of the gathering, group, examination, understanding, and presentation of data. It manages all viewpoints of this, incorporating the arranging of information accumulation in terms of the outline of overviews and investigations.
SC Calculus II (3)
Limits points are not the sole meticulous way to the organization of calculus. An elective is Abraham Robinson's non-standard dissection. Robinson's methodology, improved in the 1960s, utilizes specialized apparatus from scientific intelligence to increase the legit number framework with microscopic and limitless numbers, as in the initial Newton-Leibniz origination. The coming about numbers are c...
Limits points are not the sole meticulous way to the organization of calculus. An elective is Abraham Robinson's non-standard dissection. Robinson's methodology, improved in the 1960s, utilizes specialized apparatus from scientific intelligence to increase the legit number framework with microscopic and limitless numbers, as in the initial Newton-Leibniz origination. The coming about numbers are c...
SC Calculus I (2)
Calculus has generally been called "the math of infinitesimals", or "minute analytics". For the most part, analytics (plural calculi) points to any system or framework of count guided by the symbolic control of declarations. Certain samples of different well-known calculi are propositional analytics, variational math, lambda math, pi analytics, and unite math.
Calculus has generally been called "the math of infinitesimals", or "minute analytics". For the most part, analytics (plural calculi) points to any system or framework of count guided by the symbolic control of declarations. Certain samples of different well-known calculi are propositional analytics, variational math, lambda math, pi analytics, and unite math.
SC Calculus Reference (1)
Differential calculus is the study of the definition, lands, and requisitions of the derivative of a method. The procedure of discovering the derivative is called differentiation. Given a role and a focus in the realm, the derivative at that indicate is a way of encoding the modest-scale conduct of the role close to that indicate. By discovering the derivative of a capacity at each focus in its sp...
Differential calculus is the study of the definition, lands, and requisitions of the derivative of a method. The procedure of discovering the derivative is called differentiation. Given a role and a focus in the realm, the derivative at that indicate is a way of encoding the modest-scale conduct of the role close to that indicate. By discovering the derivative of a capacity at each focus in its sp...
RS Geometry - Shapes & Solids
Geometry is an extension of science concerned with issues of shape, size, relative position of figures, and the lands of space. A mathematician who works in the field of geometry is called a geometer. Geometry emerged autonomously in various early societies as a collection of reasonable learning concerning lengths, territories, and volumes, with components of a formal numerical science rising in t...
Geometry is an extension of science concerned with issues of shape, size, relative position of figures, and the lands of space. A mathematician who works in the field of geometry is called a geometer. Geometry emerged autonomously in various early societies as a collection of reasonable learning concerning lengths, territories, and volumes, with components of a formal numerical science rising in t...
SC Calculus I (4)
In calculus, foundations points to the thorough advancement of a subject from exact adages and definitions. In promptly calculus the utilization of microscopic amounts was thought unrigorous, and was furiously condemned by various creators, most outstandingly Michel Rolle and Priest Berkeley. Berkeley popularly depicted infinitesimals as the phantoms of withdrew amounts in his book The Investigato...
In calculus, foundations points to the thorough advancement of a subject from exact adages and definitions. In promptly calculus the utilization of microscopic amounts was thought unrigorous, and was furiously condemned by various creators, most outstandingly Michel Rolle and Priest Berkeley. Berkeley popularly depicted infinitesimals as the phantoms of withdrew amounts in his book The Investigato...
Poker Hand Odds
In poker, players develop hands of five cards as per decided ahead of time administers, which change as per which variant of poker seems to be played. The proposed hands are examined utilizing a hand ranking framework that is standard opposite all variants of poker, the player with the most noteworthy-ranking hand winning that specific bargain in most variants of poker. In certain variants, the mo...
In poker, players develop hands of five cards as per decided ahead of time administers, which change as per which variant of poker seems to be played. The proposed hands are examined utilizing a hand ranking framework that is standard opposite all variants of poker, the player with the most noteworthy-ranking hand winning that specific bargain in most variants of poker. In certain variants, the mo...
Mathematical Relationships
In arithmetic, a twofold connection on a set An is an accumulation of requested matches of components of A. In different expressions, its a subset of the Cartesian feature A2 = A × A. Ordinarily, a binary connection between two sets An and B is a subset of A × B. The terms dyadic connection and 2-place connection are synonyms for double relations. An illustration is the "partitions" connection...
In arithmetic, a twofold connection on a set An is an accumulation of requested matches of components of A. In different expressions, its a subset of the Cartesian feature A2 = A × A. Ordinarily, a binary connection between two sets An and B is a subset of A × B. The terms dyadic connection and 2-place connection are synonyms for double relations. An illustration is the "partitions" connection...
SC Calculus I (3)
The formal investigation of calculus consolidated Cavalieri's infinitesimals with the math of limited divergences advanced in Europe at around the same time. Pierre de Fermat, guaranteeing that he acquired from Diophantus, presented the idea of adequality, which acted for fairness up to a minute failure term. The synthesis was attained by John Wallis, Isaac Pushcart, and James Gregory, the last tw...
The formal investigation of calculus consolidated Cavalieri's infinitesimals with the math of limited divergences advanced in Europe at around the same time. Pierre de Fermat, guaranteeing that he acquired from Diophantus, presented the idea of adequality, which acted for fairness up to a minute failure term. The synthesis was attained by John Wallis, Isaac Pushcart, and James Gregory, the last tw...
SC Calculus II (2)
In current maths, the foundations of calculus are incorporated in the field of veritable dissection, which holds full definitions and confirmations of the theorems of calculus. The achieve of calculus has moreover been significantly amplified. Henri Lebesgue developed measure speculation and utilized it to outline integrals of all but the most obsessive roles. Laurent Schwartz presented Conveyance...
In current maths, the foundations of calculus are incorporated in the field of veritable dissection, which holds full definitions and confirmations of the theorems of calculus. The achieve of calculus has moreover been significantly amplified. Henri Lebesgue developed measure speculation and utilized it to outline integrals of all but the most obsessive roles. Laurent Schwartz presented Conveyance...
Russian Multiplication
In arithmetic, antiquated Egyptian duplication (likewise reputed to be Egyptian augmentation, Ethiopian duplication, Russian increase, or worker increase), one of two augmentation techniques utilized by recorders, was a methodical system for reproducing two numbers that does not need the increase table, just the capacity to reproduce and separation by 2, and to include. It decays one of the multip...
In arithmetic, antiquated Egyptian duplication (likewise reputed to be Egyptian augmentation, Ethiopian duplication, Russian increase, or worker increase), one of two augmentation techniques utilized by recorders, was a methodical system for reproducing two numbers that does not need the increase table, just the capacity to reproduce and separation by 2, and to include. It decays one of the multip...
International System of Units Prefixes
The Universal Framework of Units (condensed SI from French: Système worldwide d'unités) is the advanced manifestation of the metric framework. It contains a framework of units of estimation devised around seven base units and the advantage of the number ten. The SI was made in 1960, dependent upon the metre-kilogram-second framework, as opposed to the centimetre-gram-second framework, which, in tu...
The Universal Framework of Units (condensed SI from French: Système worldwide d'unités) is the advanced manifestation of the metric framework. It contains a framework of units of estimation devised around seven base units and the advantage of the number ten. The SI was made in 1960, dependent upon the metre-kilogram-second framework, as opposed to the centimetre-gram-second framework, which, in tu...
RS Calculus Integrals
Calculus Integrals is a significant notion in arithmetic and, as one with its converse, differentiation, is one of the two primary operations in analytics. Given a capacity f of a certifiable variable x and an interim [a, b] of the pure line, the decided essential
Calculus Integrals is a significant notion in arithmetic and, as one with its converse, differentiation, is one of the two primary operations in analytics. Given a capacity f of a certifiable variable x and an interim [a, b] of the pure line, the decided essential
SC Algebra I (4)
Unique algebra based maths was upgraded in the 19th century, deriving from the premium in handling examinations, from the get go fixating on what is now called Galois speculation, and on constructibility issues. The "present day polynomial maths" has significant nineteenth-century creates in the work, for example, of Richard Dedekind and Leopold Kronecker and critical interconnections with diverse...
Unique algebra based maths was upgraded in the 19th century, deriving from the premium in handling examinations, from the get go fixating on what is now called Galois speculation, and on constructibility issues. The "present day polynomial maths" has significant nineteenth-century creates in the work, for example, of Richard Dedekind and Leopold Kronecker and critical interconnections with diverse...
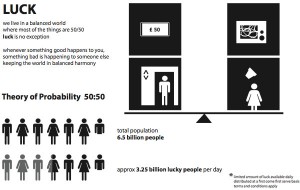
Probability of Life
Likeliness is a measure of the anticipation that an occasion will happen or a proclamation is correct. Probabilities are given a quality between 0 (should not happen) and 1 (will occur). The higher the prospect of an occasion, the more certain we are that the occasion will happen. The thought has been given a proverbial scientific induction in expectation hypothesis, which is utilized broadly ...
Likeliness is a measure of the anticipation that an occasion will happen or a proclamation is correct. Probabilities are given a quality between 0 (should not happen) and 1 (will occur). The higher the prospect of an occasion, the more certain we are that the occasion will happen. The thought has been given a proverbial scientific induction in expectation hypothesis, which is utilized broadly ...
Grok Quine
Quine's position: that goal scientific truths exist, and if there are outsiders they could perceive our math. Grok's position: that goal scientific truths don't exist, and if there are outsiders they could have no idea how to comprehend our math.
Quine's position: that goal scientific truths exist, and if there are outsiders they could perceive our math. Grok's position: that goal scientific truths don't exist, and if there are outsiders they could have no idea how to comprehend our math.
SC Calculus II (5)
In the 19th century, infinitesimals were traded by breaking points. Breaking points depict the quality of a method at a certain include in terms of its qualities at nearby enter. They catch humble-scale conduct, practically the same as infinitesimals, however utilize the normal legitimate number framework. In this medicine, calculus is an accumulation of systems for controlling certain points of c...
In the 19th century, infinitesimals were traded by breaking points. Breaking points depict the quality of a method at a certain include in terms of its qualities at nearby enter. They catch humble-scale conduct, practically the same as infinitesimals, however utilize the normal legitimate number framework. In this medicine, calculus is an accumulation of systems for controlling certain points of c...

 Upload your infographic here and contribute to our community.
Upload your infographic here and contribute to our community. 
Leave a Reply